Answer:
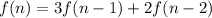 , if
, if
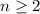 .
.
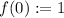 ,
,
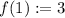
Explanation:
Let
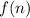 be the number of different tiling of
be the number of different tiling of
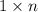 floor. We can divide all possible tiling of floor
floor. We can divide all possible tiling of floor
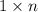 into five not overlapping groups by color of last cell in the row (Blue, Red, Green, Orange, White).
into five not overlapping groups by color of last cell in the row (Blue, Red, Green, Orange, White).
The number of tiling
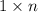 floor such that last cell in row is Blue is exactly f(n - 1) because we can throw away last
floor such that last cell in row is Blue is exactly f(n - 1) because we can throw away last
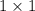 tile and cover the rest
tile and cover the rest
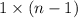 cells in f(n - 1) ways. Similarly for Red and Green.
cells in f(n - 1) ways. Similarly for Red and Green.
The number of tiling
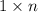 floor such that last cell in row is Orange is exactly f(n - 2) because we can throw away last
floor such that last cell in row is Orange is exactly f(n - 2) because we can throw away last
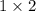 tile and cover the rest
tile and cover the rest
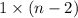 cells in f(n - 2) ways. Similarly for White.
cells in f(n - 2) ways. Similarly for White.
So we get recurrent relation:
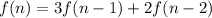 , if
, if
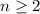 .
.
Now we should define the initial conditions.
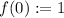 because there is only one empty tiling.
because there is only one empty tiling.
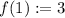 because we can place Blue, Red or Green tile.
because we can place Blue, Red or Green tile.
This completely define our recurent sequence because the depth of reccurence is 2.