Question

A 22-inch by 70-inch piece of cardboard is used to make an open-top box by removing a square from each corner of the cardboard and folding up the flaps on each side. What size square should be cut from each corner to get a box with the maximum volume

Answer 1

5 Inches

Explanation:

Let the side length of the square in inches=y.

Height of the Box = y

Since we are removing the square from both sides

• Width of the box = 22-2y
• Length of the box = 70-2y

Then the volume of the box,

`V = y(22 -2y)(70-2y) \\= 4y(y -11)(y -35)\\V = 4y^3 -184y^2 +1540y`

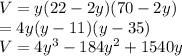
We maximize the volume of the box by taking its derivative and solving it for its critical point.

`V' = 12y^2 -368y +1540`

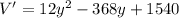
When V'=0

`12y^2 -368y +1540=0`

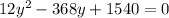
Divide all through by 4 and factor

`(3x -77)(x -5) = 0 \\3x-77=0$ or $x-5=0\\x=25.6$ or x=5`

x cannot be greater than 11. therefore, the value of x=25.6 is extraneous. The side length of the square that should be cut to maximize its volume is 5 inches.