Question

salaries of 45 college graduates who took a statistic course in college have a mean of 68,500 assuming a standard deviation, of 10,990, construct 95% confidence interval for estimating the population mean mu​

Answer 1

Step-by-step explanation:

We are given:

sample size= n = 45

sample mean = x = 61,300

sample standard deviation =18,246

Since the population standard deviation is not known we will use t distribution to find the confidence interval.

Confidence interval = 99%

Degrees of freedom= n - 1 = 45 – 1 = 44

Critical t value = 2.692

The 99% confidence interval will be:
`(x-t_(critical)* (s)/( √(n) ), x+t_(critical)* (s)/( √(n) )) \\ \\ (61300-2.692* (18246)/( √(45) ), 61300+2.692* (18246)/( √(45) )) \\ \\ (53978,68622)`

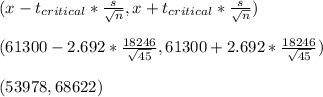
Thus, the 99% confidence interval for the population mean is:

53978 to 68622