Question

A publisher reports that 65% of their readers own a laptop. A marketing executive wants to test the claim that the percentage is actually different from the reported percentage. A random sample of 340 found that 60% of the readers owned a laptop. State the null and alternative hypotheses. Answer

Answer 1

`z=\frac{0.60 -0.65}{\sqrt{(0.65(1-0.65))/(340)}}=-1.933`

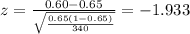
The p value for this case can be calculated with this probability:

`p_v =2*P(z<-1.933)=0.0532`

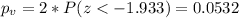
For this case is we use a significance level of 5% we have enough evidence to FAIL to reject the null hypothesis and we can't conclude that the true proportion is different from 0.65 or 65%. We need to be careful since if we use a value higher than 65 for the significance the result would change

Explanation:

Information given

n=340 represent the random sample taken

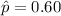`\hat p=0.60` estimated proportion of readers owned a laptop

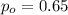`p_o=0.65` is the value that we want to test

z would represent the statistic

Alternative hypothesis:
`p \\eq 0.65`

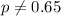
The statistic is given by:

`z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}` (1)

Replacing we got:

`z=\frac{0.60 -0.65}{\sqrt{(0.65(1-0.65))/(340)}}=-1.933`

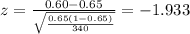
The p value for this case can be calculated with this probability:

`p_v =2*P(z<-1.933)=0.0532`

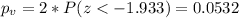
For this case is we use a significance level of 5% we have enough evidence to FAIL to reject the null hypothesis and we can't conclude that the true proportion is different from 0.65 or 65%. We need to be careful since if we use a value higher than 65 for the significance the result would change