Answer:
you should hold 76 shares of stock per 100 put options to hedge your risk.
Step-by-step explanation:
Current stock price, S = $85
Risk-free rate of return, r = 5%
Standard Deviation, v = 25%
Exercise price, X = $90
expiration date, t (in years) = 30 days = 1 month = 1/12 = 0.083333 years
The option price (OP) is given by the formula:
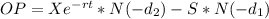
![d_1 = [ln(S/X) + (r + v^(2) /2)t]/vt^(0.5)\\d_1 = [ln(85/90) + (0.05 + 0.25^(2) /2)*0.08333]/(0.25*0.08333^(0.5))\\d_1 = -0.6982](https://img.qammunity.org/2021/formulas/business/college/2gdbqqq6u71o775j4ai4hvehi1r5pxa54r.png)
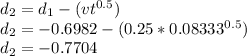
Using the pro-metric calculator for the cumulative normal distribution:
N(-d1) = N(- (-0.6982)) = N(0.6982) = 0.75747
N(-d2) = N(-(-0.7704)) = N(0.7704) = 0.77947
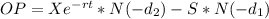
![OP =[ 90e^((-0.05*0.08333)) * 0.77947] - (85*0.75747)\\OP = 5.48](https://img.qammunity.org/2021/formulas/business/college/e8u38urpdelqqaszmm4gud4lf449am63qp.png)
Note that N(-d₁) = 0.76
This means that 76/100 (i.e to hedge your risk, you should hold 76 per 100 put options )