Question

Consider a steady developing laminar flow of water in a constant-diameter horizontal discharge pipe attached to a tank. The fluid enters the pipe with nearly uniform velocity V and pressure P1. The velocity profile becomes parabolic after a certain distance with a momentum correction factor of 2 while the pressure drops to P2. Identify the correct relation for the horizontal force acting on the bolts that hold the pipe attached to the tank.

Answer 1

hello attached is the free body diagram of the missing figure

Fr =
`(\pi )/(4) D^2 [ ( P1 - P2) - pV^2 ]`

Step-by-step explanation:

Average velocity is constant i.e V1 = V2 = V

The momentum equation for the flow in the Z - direction can be expressed as

-Fr + P1 Ac - P2 Ac = mB2V2 - mB1V1 ------- equation 1

Fr = horizontal force on the bolts

P1 = pressure of fluid at entrance

V1 = velocity of fluid at entrance

Ac = cross section area of the pipe

P2 and V2 = pressure and velocity of fluid at some distance

m = mass flow rate of fluid

B1 = momentum flux at entrance , B2 = momentum flux correction factor

Note; average velocity is constant hence substitute V for V1 and V2

equation 1 becomes

Fr = ( P1 - P2 ) Ac + mV ( 1 - 2 )

Fr = ( P1 - P2 ) Ac - mV ---------------- equation 2

equation for mass flow rate

m = pAcV

p = density of the fluid

insert this into equation 2 EQUATION 2 BECOMES

Fr = ( P1 - P2) Ac - pAcV^2

= Ac [ (P1 - P2) - pV^2 ] ---------- equation 3

Note Ac =
`(\pi )/(4) D^2`

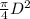
Equation 3 becomes

Fr =
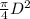`(\pi )/(4) D^2` [ (P1 -P2 ) - pV^2 ] ------- relation for the horizontal force acting on the bolts