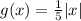Question

If you vertically compress the absolute value parent function, f(x) = [ 41, by a

factor of 5, what is the equation of the new function?
A. g(x) = 1/5 |x|
B. g(x) = |x - 5|
C. g(x) = |5x|
D. g(x) = 5|x|

Answer 1

G(x)=1/5 |x|

Explanation:

A p e x

Answer 2

`g(x) = (1)/(5) |x|`

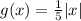
Explanation:

Given

`f(x) = |x|`

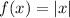
Vertically compressed

Compression Factor = 5

Required

Find the equation of the new function;

Let the new function be represented by g(x)

Let c represented the compression factor;

such that c = 5

When a function f(x) is vertically compressed by factor c, the new function becomes

`f((1)/(c)x)`

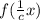
From properties of functions;

`f((1)/(c)x) = (1)/(c) *f(x)`

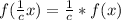
This implies that

`g(x) = f((1)/(c)x) = (1)/(c) *f(x)`

`g(x) = (1)/(c) *f(x)`

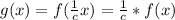
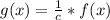
Recall that
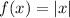`f(x) = |x|` and c = 5

`g(x) = (1)/(5) * |x|`

`g(x) = (1)/(5) |x|`

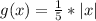
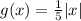
Hence, the new function is
`g(x) = (1)/(5) |x|`