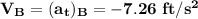Question

For the instant represented, car A has an acceleration in the direction of its motion, and car B has a speed of 45 mi/hr which is increasing. If the acceleration of B as observed from A is zero for this instant, determine the magnitude of the acceleration of A and the rate at which the speed of B is changing.

Answer 1

`\mathbf{a_A = 10.267 \ ft/s^2}`

`\mathbf{V_B = (a_t)_B =-7.26 \ ft/s^2}`

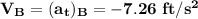
Step-by-step explanation:

Firstly, there is supposed to be a diagram attached in order to complete this question;

I have attached the diagram below in order to solve this question.

From the data given;

The radius of the car R = 600 ft

Velocity of the car B,
`V_B = 45 mi / hr`

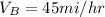
We are to determine the magnitude of the acceleration of A and the rate at which the speed of B is changing.

To start with the magnitude of acceleration A;

We all know that

1 mile = 5280 ft and an hour = 3600 seconds

Thus for ; 1 mile/hr ; we have :

5280 ft/ 3600 seconds

= 22/15 ft/sec

However;

for the velocity of the car B = 45 mi/hr; to ft/sec, we have:

= (45 × 22/15) ft/sec

= 66 ft/sec

A free body diagram is attached in the second diagram showing how we resolve the vector form

Now; to determine the magnitude of the acceleration of A; we have:

`^ \to {a_A} = a_A sin 45^0 ^(\to) + a_A cos 45^0 \ j ^(\to) \\ \\ ^\to {a_B} = -(a_t)_B \ i ^ \to + (a_c )_B cos 45 ^0 \ j ^(\to)`

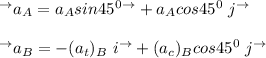
Where;

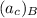`(a_c)_B` = radial acceleration of B

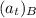`(a_t)_B` = tangential acceleration of B

From observation in the diagram; The acceleration of B is 0 from A

So;

`a_B ^\to - a_A ^\to = a_(B/A) ^ \to`

`(-(a_t)_B - a_A sin 45^0 ) ^\to i+ ((a_t)_B-a_A \ cos \ 45^0) ^ \to j = 0`

`(a_c)_B = (V_B^2)/(R)`

`(a_c)_B = ((66)^2)/(600)`

`(a_c)_B = 7.26 ft/s^2`

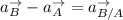
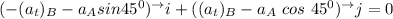
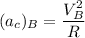
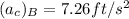
Equating the coefficient of i and j now; we have :

`(a_t)_B = -a_A \ sin 45^0 --- (1)\\ \\ (a_c)_B = a_A cos \ 45^0 --- (2)\\ \\`

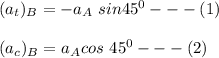
From equation (2)

replace
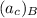`(a_c)_B` with 7.26 ft/s^2; we have

`7.26 \ ft/s^2 = a_A cos \ 45^0 \\ \\ a_A = (7.26 \ ft/s^2)/(co s \ 45^0)`

`\mathbf{a_A = 10.267 \ ft/s^2}`

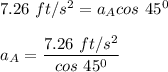
Similarly;

From equation (1)

`(a_t)_B = -a_A \ sin 45^0`

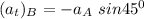
replace
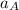`a_A` with 10.267 ft/s^2

`(a_t)_B = -10.267 \ ft/s^2 * \ sin 45^0`

`\mathbf{V_B = (a_t)_B =-7.26 \ ft/s^2}`