Answer:
The solution to the system of equations is (8,11)
Explanation:
A system of linear equations includes the line that is created by the equation y = x+ 3
The line through the points (3, 1) and (4, 3)
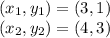
Equation of line =
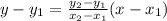
Equation of line =
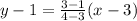
Equation of line =y-1=2x-6
Equation of line =y=2x-5
On a coordinate plane, a line goes through (0, 3) and (2, 5).

Equation of line =

Equation of line =y=2x+3
Plot all lines on graph
y = x+ 3 ---- Blue line
y=2x-5 --- Green line
y=2x+3 ---- Purple line
Refer the attached figure :
Hence the solution to the system of equations is (8,11)