Answer:
It is vertically stretched by a factor of 200 and shifted 10 units right
Explanation:
Suppose we have a function f(x).
a*f(x), a > 1, is vertically stretching f(x) a units. Otherwise, if a < 1, we are vertically compressing f(x) by a units.
f(x - a) is shifting f(x) a units to the right.
f(x + a) is shifting f(x) a units to the left.
In this question:
Initially:
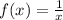
Then, first we shift, end up with:
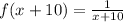
f was shifted 10 units to the left.
Finally,
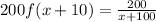
It was vertically stretched by a factor of 200.
So the correct answer is:
It is vertically stretched by a factor of 200 and shifted 10 units right