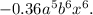Answer:
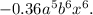
Explanation:
Given:
a²x⁵b, −0.6axb² and 0.6a²b³
Required
Find their product
The product of a²x⁵b, −0.6axb² and 0.6a²b³ is as follows:
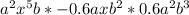
Split individual monomial
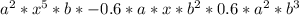
Bring like terms together
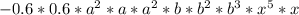
For ease of multiplication, group each like terms using brackets
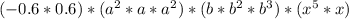
Using law of indices;
Which states that;
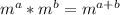
The expression becomes:
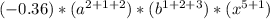
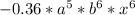
Multiply the above expression
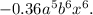
Hence;
The product of a²x⁵b, −0.6axb² and 0.6a²b³ is equivalent to