Question

Show that every triangle formed by the coordinate axes and a tangent line to y = 1/x ( for x > 0)

always has an area of 2 square units.

Hint: Find the equation of the tangent line at x = a. (It will contain a’s as well as x and y.) Then find the

x-and y-intercepts for that line to find the lengths of sides of the right triangle.

Answer 1

Explanation:

given a point
`(x_0,y_0)` the equation of a line with slope m that passes through the given point is

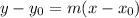`y-y_0 = m(x-x_0)` or equivalently

`y = mx+(y_0-mx_0)`.

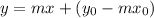Recall that a line of the form
`y=mx+b`, the y intercept is b and the x intercept is
`(-b)/(m)`.

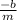So, in our case, the y intercept is
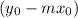`(y_0-mx_0)` and the x intercept is
`(mx_0-y_0)/(m)`.

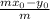In our case, we know that the line is tangent to the graph of 1/x. So consider a point over the graph
`(x_0,(1)/(x_0))`. Which means that
`y_0=(1)/(x_0)`

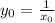
The slope of the tangent line is given by the derivative of the function evaluated at
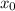`x_0`. Using the properties of derivatives, we get

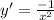`y' = (-1)/(x^2)`. So evaluated at
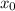`x_0` we get
`m = (-1)/(x_0^2)`

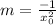
Replacing the values in our previous findings we get that the y intercept is

`(y_0-mx_0) = ((1)/(x_0)-((-1)/(x_0^2)x_0)) = (2)/(x_0)`

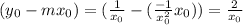
The x intercept is

`(mx_0-y_0)/(m) = ((-1)/(x_0^2)x_0-(1)/(x_0))/((-1)/(x_0^2)) = 2x_0`

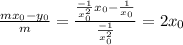
The triangle in consideration has height
`(2)/(x_0)` and base
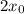`2x_0`. So the area is

`(1)/(2)(2)/(x_0)\cdot 2x_0=2`

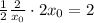
So regardless of the point we take on the graph, the area of the triangle is always 2.