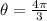Answer:
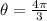
Explanation:
Given
Let A represent the Length of Arc CD and C, represents the circumference
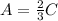
Required
Find the central angle (in radians)
The length of arc CD in radians is as follows;

Where r is the radius and
 is the measure of central angle
is the measure of central angle
The circumference of a circle is calculated as thus;
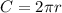
From the question, it was stated that the arc length is 2-3rd of the circumference;
This means that
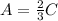
Substitute
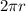 for C and
for C and
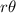 for A
for A
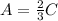 becomes
becomes
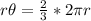

Divide both sides by r
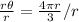
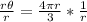
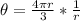
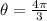
Hence, the measure of the central angle;