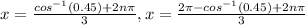Question

Solve 2cos3x=0.9.

Pls help me with this trigonometric equations with multiple angles.

Answer 1

`x=(cos^(-1)(0.45)+2n\pi)/(3) ,x=(2\pi- cos^(-1)(0.45)+2n\pi)/(3)`

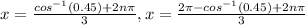
Explanation:

Given:
`2 cos(3x)=0.9`

To find: solutions of the given equation

Solution:

Triangle is a polygon that has three sides, three angles and three vertices.

Trigonometry explains relationship between the sides and the angles of the triangle.

Use the fact:
`cos x=a`⇒
`x=cos^(-1)(a)+2n\pi,x=2\pi-cos^(-1)(a)+2n\pi`

`2 cos(3x)=0.9`

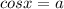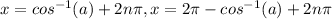
Divide both sides by 2

`cos(3x)=(0.9)/(2)=0.45`

`3x=cos^(-1)(0.45)+2n\pi,3x=2\pi- cos^(-1)(0.45)+2n\pi`

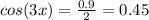
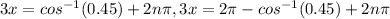
So,

`x=(cos^(-1)(0.45)+2n\pi)/(3) ,x=(2\pi- cos^(-1)(0.45)+2n\pi)/(3)`