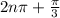Question

Find all solutions of the equation in the interval [0, 2π). cos x + sin x tan x = 2

Answer 1

The solutions of the equation in the interval [0,2π )

={
`(\pi )/(3)` }

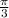General solution θ = 2 nπ +α

θ =
`2n\pi + (\pi )/(3)`

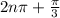
Explanation:

Step(i):-

Given equation

cos x + sin x tan x = 2

⇒
`cos x + sin x (sin x)/(cos x) = 2`

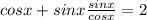
On simplification , we get

⇒
`(sin^(2) x+ cos^2x)/(cos x) = 2`

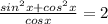
we know that trigonometry formula

`sin^(2) x+ cos^2 x = 1`

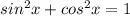
now we get

`(1)/(cos x) = 2`

⇒
`cos x = (1)/(2)`

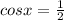
⇒ cos x = cos 60°

Step(ii):-

General solution of cosθ = cosα

General solution θ = 2 nπ +α

θ = 2 nπ +60°

θ =
`2n\pi + (\pi )/(3)`

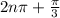
put n = 0 ⇒ θ = 60°

Put n =1 ⇒ θ = 360°+60°= 420°

.....and so on

The solutions of the equation in the interval =
`(\pi )/(3)`

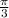
Final answer:-

The solutions of the equation in the interval [0,2π )

={
`(\pi )/(3)` }

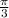General solution θ = 2 nπ +α

θ =
`2n\pi + (\pi )/(3)`