Answer:
The 75th percentile of this distribution is 11 .25 minutes.
Explanation:
The random variable X is defined as the waiting time in line at an ice cream shop.
The random variable X follows a Uniform distribution with parameters a = 3 minutes and b = 14 minutes.
The probability density function of X is:
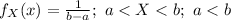
The pth percentile is a data value such that at least p% of the data-set is less than or equal to this data value and at least (100-p)% of the data-set are more than or equal to this data value.
Then the 75th percentile of this distribution is:
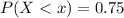
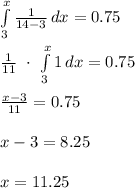
Thus, the 75th percentile of this distribution is 11 .25 minutes.