Question

1. For ball bearings, determine: (a) The factor by which the catalog rating (C10) must be increased, if the life of a bearing under a constant load is to double. Use equation 11-1 as your starting point. (b) Given the Weibull parameters of example 11-3, the factor by which the catalog rating must be increased if the reliability is to be increased from 0.9 to 0.99.

Answer 1

(b) Given the Weibull parameters of example 11-3, the factor by which the catalog rating must be increased if the reliability is to be increased from 0.9 to 0.99.

Equation 11-1: F*L^(1/3) = Constant

Weibull parameters of example 11-3: xo = 0.02 (theta-xo) = 4.439 b = 1.483

Step-by-step explanation:

(a)The Catalog rating(C)

Bearing life:
`L_1 = L , L_2 = 2L`

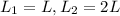
Catalog rating:
`C_1 = C , C_2 = ? ,`

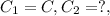
From given equation bearing life equation,

`F*(1)/(3) (L_1) = C_1 ...(1) \\\\ F*(1)/(3) (L_2) =C_2...(2)`

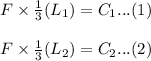
we Dividing eqn (2) with (1)

`(C_2)/(C_1) =(1)/(3) ((L_2)/(L_1))\\\\ C_2 = C*((2L)/(L))(1)/(3) \\\\ C_2 = 1.26 C`

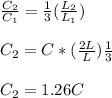
The Catalog rating increased by factor of 1.26

(b) Reliability Increase from 0.9 to 0.99

`R_1 = 0.9 , R_2 = 0.99`

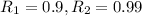
Now calculating life adjustment factor for both value of reliability from Weibull parametres

`a_1 = x_o + (\theta - x_o){ ln((1)/(R_1) ) }^{(1)/(b)}`

`= 0.02 + 4.439{ ln((1)/(0.9) ) }^{(1)/(1.483)} \\\\ = 0.02 + 4.439( 0.1044 )^(0.67)\\\\a_1 = 0.9968`

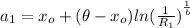
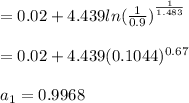
Similarly

`a_2 = x_o + (\theta - x_o){ ln((1)/(R_2) ) }^{(1)/(b) }\\\\ = 0.02 + 4.439{ ln(1/0.99) }^{(1)/(1.483) }\\\\ = 0.02 + 4.439( 0.0099 )^(0.67)\\\\a_2 = 0.2215`

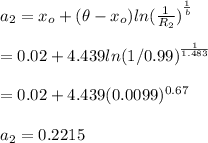
Now calculating bearing life for each value

`L_1 = a_1 * LL_1 = 0.9968LL_2 = a_2 * LL_2 = 0.2215L`

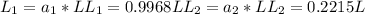
Now using given ball bearing life equation and dividing each other similar to previous problem

`(C_2)/(C_1) = ((L_2)/(L_1) )^{(1)/(3) }\\\\ C_2 = C* ((0.2215L )/(0.9968L) )^(1/3)\\\\ C_2 = 0.61 C`

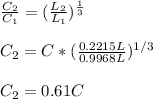
Catalog rating increased by factor of 0.61