Question

Given f(x) = 1/x+4 and
g(x) = 8/x-1, find the given domain of f(g(x)).

Answer 1

he domain of the composition is all real x values except for x = -1

In other words:
`\left \\, x \\eq -1 \right \}`

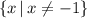
Explanation:

Let's find the composition
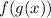`f(g(x))` in order to answer about its domain (where on the Real number set the function is defined), give the two functions:

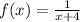`f(x)= (1)/(x+4)` and
`g(x)=(8)/(x-1)` :

`f(g(x))=(1)/(g(x)+4) \\f(g(x))=(1)/((8)/(x-1) +4) \\f(g(x))=(1)/((8+4(x-1))/(x-1) )\\f(g(x))=(x-1)/(8+4x-4) \\f(g(x))=(x-1)/(4+4x) \\`

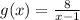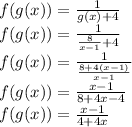
This rational function is defined for every real number except when the denominator adopts the value zero. Such happens when:

`4+4x=0\\4x=-4\\x=-1`

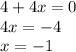
So the domain of the composition is all real x values except for x = -1