Question

- Let f(x)= -6x + 3 and g(x) = 5x + 4. Find f•g and state its domain.

A: -30x^2 - 9x + 12; all real numbers except x = 4

B: -30x^2 - 9x + 12; all real numbers

C: -18x^2 - 39x + 20; all real numbers

D: -18x^2 - 39x + 20; all real numbers except x = 1

Answer 1

The function is
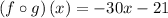`\left(f \circ g \right) \left( x \right) = - 30 x - 21` and the domain is all real numbers.

Explanation:

Composition of functions is when one function is inside of another function.

The notation used for the composition of functions looks like this,
`\left(f \circ g \right) \left( x \right) = f(g(x))`.

We have the following functions

`f(x)= -6x + 3\\\\g(x) = 5x + 4`

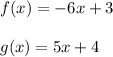
The composite function is

`\left(f \circ g \right) \left( x \right) = f \left( g \left( x \right) \right)=f \left(5 x + 4 \right) = 3 - 6 {\left(5 x + 4\right)} = - 30 x - 21`.

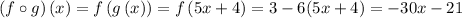The domain is the set of all possible x-values which will make the function "work", and will output real y-values.

The function
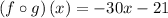`\left(f \circ g \right) \left( x \right) = - 30 x - 21` has no undefined points nor domain constraints. Therefore, the domain is
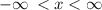`-\infty \:<x<\infty \:` or all real numbers.