Answer:
Answer C:
Cannot be true because
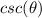 is greater than zero in quadrant 2.
is greater than zero in quadrant 2.
Explanation:
When the csc of an angle is negative, since the cosecant function is defined as:
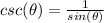
that means that the sin of the angle must be negative, and such cannot happen in the second quadrant. The sine function is positive in the first and second quadrant.
Therefore, the correct answer is:
Cannot be true because
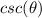 is greater than zero in quadrant 2.
is greater than zero in quadrant 2.