Answer:
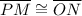 : Reason; Corresponding parts of congruent triangles ΔOMN and ΔOMP are congruent (CPCTC)
: Reason; Corresponding parts of congruent triangles ΔOMN and ΔOMP are congruent (CPCTC)
Explanation:
1) MNOP is a parallelogram: Reason; Given
2)
 : Reason; Definition of a parallelogram
: Reason; Definition of a parallelogram
3) ∠MON ≅ ∠PMO: Reason; Alternate Int. ∠s Thm.
4)
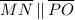 : Reason; Definition of a parallelogram
: Reason; Definition of a parallelogram
5) ∠NMO ≅ ∠POM: Reason; Alternate Int. ∠s Thm.
6)
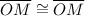 : Reason; Reflexive property
: Reason; Reflexive property
7) ΔOMN ≅ ΔOMP: Reason; Angle Angle Side (AAS) congruency theorem
8)
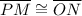 : Reason; Corresponding parts of congruent triangles are congruent (CPCTC).
: Reason; Corresponding parts of congruent triangles are congruent (CPCTC).
Also we have;
9)
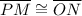 : Reason; Segment opposite congruent angles are congruent
: Reason; Segment opposite congruent angles are congruent