Question

The average life of Canadian women is 72.90 years, and the standard deviation of the life expectancy of Canadian women is 8 years. Based on Chebyshev's Theorem, determine the upper and lower bounds on the average life expectancy of Canadian women such that at least 95 percent of the population is included if the sample size is 100 women.

Answer 1

Answer: The lower bound is 37.124 years and upper bound is 108.676 years.

Step-by-step explanation:

Since we have given that

Mean = 72.90

Standard deviation = 8

At least 95% of population is included.

N = 100

Using Chebyshev's theorem, we have

`100(1-(1)/(t^2))\%=95\\\\(1-(1)/(t^2))=0.95\\\\(1)/(t^2)=0.05\\\\t^2=(1)/(0.05)=20\\\\t=4.472`

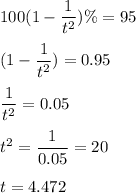
So, the interval would be

`(\mu-t\sigma,\mu+t\sigma)\\\\=(72.90-4.472* 8,72.90+4.472* 8)\\\\=(37.124,108.676)`

Hence, the lower bound is 37.124 years and upper bound is 108.676 years.