Question

In a study of 905 randomly selected children aged 15-17, 198 say they watch 3 or more hours of television per day. In a study of 503 randomly selected children aged 12-14, 97 reported they watch 3 or more hours of television per day. Is there a significant difference between age and watching television in teenagers

Answer 1

The calculated value Z = 0.063< 1.96 at 5% level of significance

Null hypothesis is accepted

There is no significant difference between age and watching television in teenagers

Explanation:

Step(i):-

Given random sample size 'n' = 905

Given data 198 say they watch 3 or more hours of television per day.

Given random first sample size

n₁ = 905

First sample proportion

`p_(1) = (x_(1) )/(n_(1) ) = (198)/(905) = 0.2187`

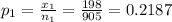
Given random second sample size

n₂ = 503

second sample proportion

`p_(2) = (x_(2) )/(n_(1) ) = (97)/(503) = 0.1928`

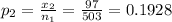
Step(ii):-

Null Hypothesis : H₀

There is no significant difference between age and watching television in teenagers

Alternative Hypothesis :H₁

There is significant difference between age and watching television in teenagers

Step(iii):-

Test statistic

`Z = \frac{p_(1)-p_(2) }{\sqrt{PQ((1)/(n_(1) )+(1)/(n_(2) ) }) }`

Where

`P = (n_(1)p_(1) + n_(2) p_(2) )/(n_(1)+n_(2) )`

`P = (905 X0.2187 + 503 X0.1928 )/(905+503 )`

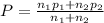
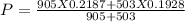
P = 0.2094

Q = 1 - 0.2094 = 0.7906

`Z = \frac{0.2187-0.1928}{\sqrt{0.2094 X0.7906((1)/(905) +(1)/(503) } )}`

on calculation , we get

Z = 0.063

The critical value Z₀.₀₅ = 1.96

The calculated value Z = 0.063< 1.96 at 5% level of significance

Conclusion:-

Null hypothesis is accepted

There is no significant difference between age and watching television in teenagers