Answer:
A volume of a cubic meter of water from the surface of the lake has been compressed in 0.004 cubic meters.
Step-by-step explanation:
The bulk modulus is represented by the following differential equation:
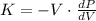
Where:
 - Bulk module, measured in pascals.
- Bulk module, measured in pascals.
 - Sample volume, measured in cubic meters.
- Sample volume, measured in cubic meters.
 - Local pressure, measured in pascals.
- Local pressure, measured in pascals.
Now, let suppose that bulk remains constant, so that differential equation can be reduced into a first-order linear non-homogeneous differential equation with separable variables:
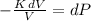
This resultant expression is solved by definite integration and algebraic handling:
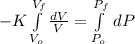
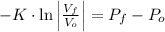

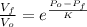
The final volume is predicted by:
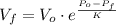
If
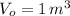 ,
,
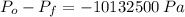 and
and
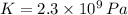 , then:
, then:
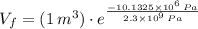
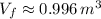
Change in volume due to increasure on pressure is:
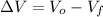
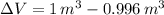
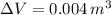
A volume of a cubic meter of water from the surface of the lake has been compressed in 0.004 cubic meters.