Question

The weight of an organ in adult males has a bell shaped distribution with a mean of 325 grams and a standard deviation of 50 grams. (A) about 99.7% of organs will be between what weights? (B) what percentage of organs weighs between 275 grams and 375? (C) what percentage of organs weighs between 275 grams and 425 grams?

Answer 1

A)

The number of weights of an organ in adult males = 374.85

B)

The percentage of organs weighs between 275 grams and 375

P(275≤x≤375) = 0.6826 = 68%

C)

The percentage of organs weighs between 275 grams and 425

P(275≤x≤375) = 0.8185 = 82%

Explanation:

A)

Step(i):-

Given mean of the normal distribution = 325 grams

Given standard deviation of the normal distribution = 50 grams

Given Z- score = 99.7% = 0.997

`Z = (x-mean)/(S.D) = (x-325)/(50)`

`0.997 = (x-325)/(50)`

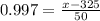
Cross multiplication , we get

`0.997 X 50= x-325`

x - 325 = 49.85

x = 325 + 49.85

x = 374.85

The number of weights of an organ in adult males = 374.85

Step(ii):-

B)

Let X₁ = 275 grams

`Z_(1) = (x_(1) -mean)/(S.D) = (275-325)/(50) = -1`

Let X₂ = 375 grams

`Z_(2) = (x_(2) -mean)/(S.D) = (375-325)/(50) = 1`

The probability of organs weighs between 275 grams and 375

P(275≤x≤375) = P(-1≤Z≤1)

= P(Z≤1)- P(Z≤-1)

= 0.5 + A(1) - ( 0.5 - A(-1))

= A(1) + A(-1)

= 2 A(1)

= 2 × 0.3413

= 0.6826

The percentage of organs weighs between 275 grams and 375

P(275≤x≤375) = 0.6826 = 68%

C)

Let X₁ = 275 grams

`Z_(1) = (x_(1) -mean)/(S.D) = (275-325)/(50) = -1`

Let X₂ = 425 grams

`Z_(2) = (x_(2) -mean)/(S.D) = (425-325)/(50) = 2`

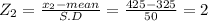
The probability of organs weighs between 275 grams and 425

P(275≤x≤425) = P(-1≤Z≤2)

= P(Z≤2)- P(Z≤-1)

= 0.5 + A(2) - ( 0.5 - A(-1))

= A(2) + A(-1)

= A(2) + A(1) (∵A(-1) =A(1)

= 0.4772 + 0.3413

= 0.8185

The percentage of organs weighs between 275 grams and 425

P(275≤x≤375) = 0.8185 = 82%