Answer:
The value of
 is given by
is given by
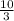 . Hence, the answer is A.
. Hence, the answer is A.
Explanation:
This exercise represents a case where the Newton-Raphson method is used, whose formula is used for differentiable function of the form
 . The expression is now described:
. The expression is now described:
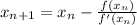
Where:
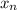 - Current approximation.
- Current approximation.
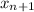 - New approximation.
- New approximation.
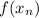 - Function evaluated in current approximation.
- Function evaluated in current approximation.
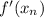 - First derivative of the function evaluated in current approximation.
- First derivative of the function evaluated in current approximation.
If
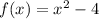 , then
, then
 . Now, given that
. Now, given that
 , the function and first derivative evaluated in
, the function and first derivative evaluated in
 are:
are:
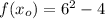
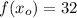
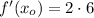
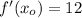
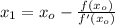
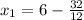
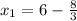


The value of
 is given by
is given by
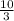 . Hence, the answer is A.
. Hence, the answer is A.