Question

Two metal bars experience an equal change in volume due to an equal change in temperature. The first bar has a coefficient of expansion twice as large as the second bar. How does the original volume of the first bar compare to the original volume of the second bar

Answer 1

The original volume of the first bar is half of the original volume of the second bar.

Step-by-step explanation:

The coefficient of cubic expansivity of substances is given by;

γ = ΔV ÷ (
`V_(1)`Δθ)

Given: two metal bars with equal change in volume, equal change in temperature.

Let the volume of the first metal bar be represented by
`V_(1)`, and that of the second by
`V_(2)`.

Since they have equal change in volume,

Δ
`V_(1)` = Δ
`V_(2)` = ΔV

For the first metal bar,

2γ = ΔV ÷ (
`V_(1)`Δθ)

⇒ Δθ = ΔV ÷ (2γ
`V_(1)`)

For the second metal bar,

γ = ΔV ÷ (
`V_(2)`Δθ)

⇒ Δθ = ΔV ÷ (
`V_(2)`γ)

Since they have equal change in temperature,

Δθ of first bar = Δθ of the second bar

ΔV ÷ (2γ
`V_(1)`) = ΔV ÷ (
`V_(2)`γ)

So that;

(1 ÷ 2
`V_(1)`) = (1 ÷
`V_(2)`)

2
`V_(1)` =
`V_(2)`

`V_(1)` =
`(V_(2) )/(2)`

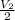
Thus, original volume of the first bar is half of the original volume of the second bar.