Question

The magnitude of the gravitational field strength near Earth's surface is represented by

Answer 1

The magnitude of the gravitational field strength near Earth's surface is represented by approximately
`9.82\,(m)/(s^(2))`.

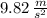Step-by-step explanation:

Let be M and m the masses of the planet and a person standing on the surface of the planet, so that M >> m. The attraction force between the planet and the person is represented by the Newton's Law of Gravitation:

`F = G\cdot (M\cdot m)/(r^(2))`

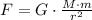
Where:

`M` - Mass of the planet Earth, measured in kilograms.

`m` - Mass of the person, measured in kilograms.

`r` - Radius of the Earth, measured in meters.

`G` - Gravitational constant, measured in
`(m^(3))/(kg\cdot s^(2))`.

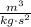But also, the magnitude of the gravitational field is given by the definition of weight, that is:

`F = m \cdot g`

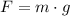
Where:

`m` - Mass of the person, measured in kilograms.

`g` - Gravity constant, measured in meters per square second.

After comparing this expression with the first one, the following equivalence is found:

`g = (G\cdot M)/(r^(2))`

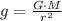
Given that
`G = 6.674* 10^(-11)\,(m^(3))/(kg\cdot s^(2))`,
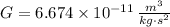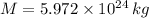`M = 5.972 * 10^(24)\,kg` and
`r = 6.371 * 10^(6)\,m`, the magnitude of the gravitational field near Earth's surface is:

`g = (\left(6.674* 10^(-11)\,(m^(3))/(kg\cdot s^(2)) \right)\cdot (5.972* 10^(24)\,kg))/((6.371* 10^(6)\,m)^(2))`

`g \approx 9.82\,(m)/(s^(2))`

The magnitude of the gravitational field strength near Earth's surface is represented by approximately
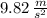`9.82\,(m)/(s^(2))`.