Question

The manager of a warehouse would like to know how many errors are made when a product’s serial number is read by a bar-code reader. Six samples are collected of the number of scanning errors: 36, 14, 21, 39, 11, and 2 errors, per 1,000 scans each.

Just to be sure, the manager has six more samples taken:


33, 45, 34, 17, 1, and 29 errors, per 1,000 scans each


How do the mean and standard deviation change, based on all 12 samples?

Answer 1

The mean and standard deviation changed to 23.5 and 14.62 respectively, based on all 12 samples.

Explanation:

We are given that the Six samples are collected of the number of scanning errors: 36, 14, 21, 39, 11, and 2 errors, per 1,000 scans each.

Representing the data in tabular form;

X
`X - \bar X`
`(X - \bar X)^(2)`

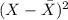
36 36 - 20.5 = 15.5 240.25

14 14 - 20.5 = -6.5 42.25

21 21 - 20.5 = 0.5 0.25

39 39 - 20.5 = 18.5 342.25

11 11 - 20.5 = -9.5 90.25

2 2 - 20.5 = -18.5 342.25

Total 1057.5

Now, the mean of these value is given by;

Mean,
`\bar X` =
`(\sum X)/(n)`

=
`(36+14+21+39+11+2)/(6)`

=
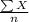
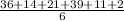
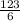`(123)/(6)` = 20.5

Standard deviation formula for discrete distribution is given by;

Standard deviation,
`\sigma` =
`\sqrt{(\sum (X -\bar X)^(2) )/(n-1) }`

=
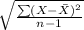
`\sqrt{(1057.5 )/(6-1) }` = 14.54

Now, the manager has six more samples taken:

33, 45, 34, 17, 1, and 29 errors, per 1,000 scans each

So, the modified table would be;

X
`X - \bar X`
`(X - \bar X)^(2)`

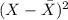
36 36 - 23.5 = 12.5 156.25

14 14 - 23.5 = -9.5 90.25

21 21 - 23.5 = -2.5 6.25

39 39 - 23.5 = 15.5 240.25

11 11 - 23.5 = -12.5 156.25

2 2 - 23.5 = -21.5 462.25

33 33 - 23.5 = 9.5 90.25

45 45 - 23.5 = 21.5 462.25

34 34 - 23.5 = 10.5 110.25

17 17 - 23.5 = -6.5 42.25

1 1 - 23.5 = -22.5 506.25

29 29 - 23.5 = 5.5 30.25

Total 2353

Now, the mean of these value is given by;

Mean,
`\bar X` =
`(\sum X)/(n)`

=
`(36+14+21+39+11+2+33+45+34+17+1+29)/(12)`

=
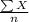
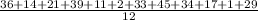
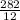`(282)/(12)` = 23.5

Standard deviation formula for discrete distribution is given by;

Standard deviation,
`\sigma` =
`\sqrt{(\sum (X -\bar X)^(2) )/(n-1) }`

=
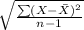
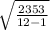`\sqrt{(2353 )/(12-1) }` = 14.62