Question

Thanks for the help!​

Answer 1

I. and II. are correct

Explanation:

The line y=0 is a horizontal asymptote in both directions, so ...

`\lim\limits_(x\to -\infty){f(x)}=\lim\limits_(x\to\infty){f(x)}=0`

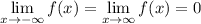
The function value f(0) is 0, so the limit is the same from either direction:

`\lim\limits_(x\to 0^-){f(x)}=\lim\limits_(x\to 0^+){f(x)}=0`

__

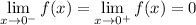
The expression for statement III can be simplified:

`(f(x)-(1)/(2))/(x-1)=((x)/(1+x^2)-(1)/(2))/(x-1)=(2x-(1+x^2))/(2(1+x^2)(x-1))=(-(x-1)^2)/(2(x-1)(x^2+1))\\\\=(1-x)/(2(x^2+1))`

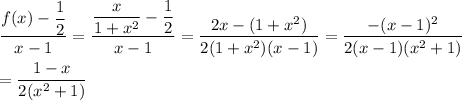
The limit of this is 0 from either direction, so the limit does exist at x=1.

_____

We consider that ...

both statements I. and II. are correct.