Question

Please help! thanks so much​

Answer 1

`\displaystyle \lim_(x \to 2) (x)/(f(x)+1) = +\infty`

Explanation:

From the graph, we can see that:

`\displaystyle \lim_(x \to 2) f(x)= -1`

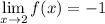
From direct substitution, we have that:

`\displaystyle \lim_(x \to 2) (x)/(f(x)+1)\Rightarrow ((2))/(-1+1)`

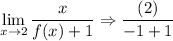
Evaluate:

`\displaystyle = (2)/(0)=\text{Und.}`

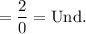
Saying undefined (or unbounded) would be correct.

However, note that as x approaches two, the value of y decreases in order to get to negative one. In other words, our function f will always be greater or equal to negative one (you can also see this from the graph). This means that as x approaches two, f(x) will approach -0.99, -0.999 and -0.9999 and so on until it reaches negative one and then go back up. Importantly, because of this, we can state that:

`\displaystyle \lim_(x \to 2) (x)/(f(x)+1)=((2))/(-1+1) = +\infty`

This is because for the denominator, the +1 will always be greater than the f(x). This makes this increase towards positive infinity. Note that limits want the values of the function as it approaches it, not at it.