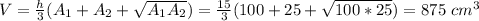Answer:
The answer is given below
Explanation:
The question is not complete. The correct question is:
A square based pyramid have a height of 30 cm and base of 10 cm. The The square based pyramid is cut horizontally at a height of 15cm to leave this frustum.
Answer:
The frustum would have a base of 10 cm and height of 15 cm. The lower base has a length of 10 cm. to calculate the upper base, we use the formula:

Substituting:
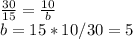
The volume of the frustum is given by the formula:
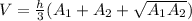
Where h is the height of the frustum = 15 cm, A1 is the area of the lower base = 10 * 10 = 100 cm², A1 is the area of the upper base = 5 * 5 = 25 cm²
Substituting gives: