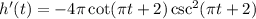Answer:
Part B)
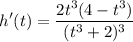
Part C)
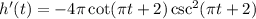
Step-by-Step Explanation:
Question B)
We have:
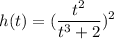
And we want to find the derivative, h‘(t).
This will require the chain rule and the quotient rule. Remember that the chain rule states:
![\displaystyle (d)/(dx)[(u(v(x))]=u^\prime(v(x))\cdot v^\prime(x)](https://img.qammunity.org/2021/formulas/mathematics/middle-school/llceto0pe9o9zna9zsr4g7ggr371j47g1a.png)
And the quotient rule:
![\displaystyle (d)/(dx)[(u)/(v)]=(u^\prime v-uv^\prime)/(v^2)](https://img.qammunity.org/2021/formulas/mathematics/middle-school/8831mffrwolu7eno4s92skyhqh6rkow47n.png)
Therefore, for our function h(t), we can let, by the chain rule:
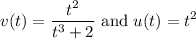
Then by the quotient rule:
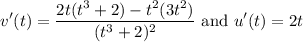
Then, by the chain rule, our derivative, h’(t), is:
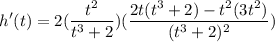
Simplify:
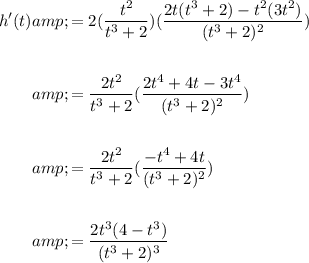
Part C)
We have:
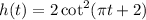
Again, we will utilize the chain rule. This time, we will let:
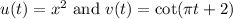
Then differentiating gives (on the right, we will apply the chain rule a second time):
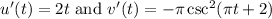
To differentiate v(t), as mentioned, we need to apply the chain rule. We have:

We will let:

Therefore:

So:
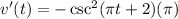
And by simplification:
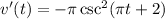
Therefore, it follows that:
![h^\prime(t)=2[2(\cot(\pi t+2))(-\pi \csc^2(\pi t+2))]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/ntly7t6wku2jky2hfst3myksu3goupknr6.png)
So: