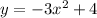Question

The equation y=3x^2=3 is graphed below on Graph A. What is the equation graphed on Graph B?

Answer 1

`y = -3x^2 + 4`

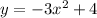
Explanation:

Hello!

The equation of a parabola is written as
`y = ax^2 + bx + c`.

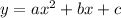Y-intercept

The
`c` value of the equation determines the y-intercept, or where the graph hits the y-axis (x = 0).

In Graph A we can see that the graph hits the y-axis at -3, showing the y-intercept is also -3. We can use the same logic to determine the y-intercept of Graph B. We can see that it hits the y-axis at 4, so the y-intercept is 4.

A-value

The
`a` value determines the direction and width of the graph. If it is positive, it opens up. If it's negative, it opens down.

Since Graph B opens down, we can simply add a negative sign to indicate that it is a negative graph.

Equation

We can plug in the values that we solved for
`a` and
`c`.

Equation:
`y = -3x^2 + 4`

Answer 2

Equation given in graph B → y = -3x² + 4

Explanation:

Equation of the graph A,

y = 3x² - 3

We have to find the equation of the graph (parabola) given in graph (B).

Parabola given in graph B is the inverted form of graph A with vertex at (0, 4)

Therefore, equation of the parabola given in graph B will be,

y = -a(x - h)² + k

where negative notation of the coefficient a shows the inverted form of the parabola given in graph A and (h, k) will be the vertex.

y = -3(x - 0)² + 4

y = -3x² + 4