Answer:
The probability that one red chip was selected is 0.0053.
Explanation:
Let the random variable X be defined as the number of red chips selected.
It is provided that the selections of the n = 5 chips are done with replacement.
This implies that the probability of selecting a red chip remains same for each trial, i.e. p = 6/9 = 2/3.
The color of the chip selected at nth draw is independent of the other selections.
The random variable X thus follows a binomial distribution with parameters n = 5 and p = 2/3.
The probability mass function of X is:
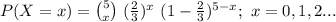
Compute the probability that one red chip was selected as follows:


Thus, the probability that one red chip was selected is 0.0053.