Question

Kong made a scale drawing of a fish tank.The tank which is 24 feet long in real life, is 12 inches long in the drawing. What scale did Kong use for the drawing? 1 inch = feet.

Answer 1

`1\ inch = 2\ feet`

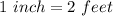
Explanation:

Given:

`Real\ tank\ measurement\ = 24\ feet`

`Scale\ measurement\ = 12\ inches`

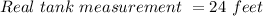
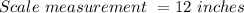
Required:

Scale Ratio.

To get the scale ratio, we simply divide the actual measurement by the scale measurement

This is done as follows:

`Scale\ Ratio = (Actual\ Measurement)/(Scale\ Measurement)`

`Scale\ Ratio\ = (24\ feet)/(12\ inches)`

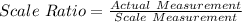
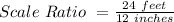
[Divide numerator and denominator by 12]

`Scale\ Ratio\ = (2\ feet)/(1\ inch)`

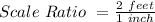
[Convert the above expression to ratio]

`Scale\ Ratio = 2\ feet : 1\ inch`

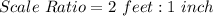
The interpretation of this is that 1 inch on the scale measurement represent 2 feet on the actual measurements