Question

Scenario: A corporation randomly selects 150 sales people and finds that 66% who have never taken a self-improvement course would like such a course. The firm did a similar study 10 years ago in which 60% of a random sample of 160 sales people wanted a self-improvement course. The groups are assumed to be independent random samples. Let straight pi subscript 1 space and space straight pi subscript 2 represent the true proportion of workers who would like to attend a self-improvement course in the recent study and the past study respectively. What is the value of the test statistic to use in evaluating the alternative hypothesis that there is a difference in the two population proportions using alpha equals 0.10

Answer 1

The calculated Z = 1.2 < 1.645 at 0.1 level of significance

Null hypothesis is accepted

There is a no difference in the two population proportions using alpha equals 0.10

Explanation:

Given first sample size n₁ = 150

Given first sample proportion p₁ = 0.66

Given second sample size n₂ = 160

Given second sample proportion p₂ = 0.60

Null hypothesis :H₀: p₁ = p₂

Alternative Hypothesis: H₁:p₁ ≠ p₂

Test statistic

`Z = \frac{p_(1) - p_(2) }{\sqrt{PQ((1)/(n_(1) )+(1)/(n_(2) ) ) } }`

Where

`P =(n_(1)p_(1) +n_(2) p_(2) )/(n_(1) +n_(2) ) = (150 X 0.66+160 X0.60)/(150+160) = 0.629`

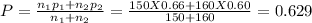
Q = 1- P = 1- 0.629 = 0.371

`Z = \frac{0.66 - 0.60 }{\sqrt{0.629 X0.371((1)/(150 )+(1)/(160) ) } }`

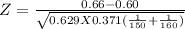
Z = 1.2

Level of significance ∝=0.1

The critical value at ∝=0.1

`Z_(0.10) = 1.645`

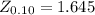
The calculated Z = 1.2 < 1.645 at 0.1 level of significance

Null hypothesis is accepted

There is a no difference in the two population proportions using alpha equals 0.10