Question

A supplier of heavy construction equipment has found that new customers are normally obtained through customer requests for a sales call and that the probability of a sale of a particular piece of equipment is 0.15. If the supplier has four pieces of the equipment available for sale, what is the probability that it will take fewer than six customer contacts to clear the inventory?

Answer 1

The probability that it will take fewer than six customer contacts to clear the inventory is 0.8%.

Explanation:

We have a probability of making an individual sale of p=0.15.

We have 4 units, so the probability of clearing the inventory with n clients can be calculated as:

`P=\dbinom{n}{4}p^4q^(n-4)=\dbinom{n}{4}0.15^4\cdot 0.85^(n-4)`

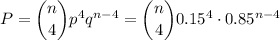
As we see in the equation, n has to be equal or big than 4.

In this problem we have to calculate the probability that less than 6 clients are needed to sell the 4 units.

This probability can be calculated adding the probability from n=4 to n=6:

`P=\sum_(n=4)^6P(n)=\sum_(n=4)^6 \dbinom{n}{4}0.15^4^\cdot 0.85^(n-4)\\\\\\P=0.15^4((4!)/(4!0!)\cdot 0.85^(4-4)+(5!)/(4!1!)\cdot0.85^(5-4)+(6!)/(4!2!)0.85^(6-4))\\\\\\P=0.15^4(1\cdot0.85^0+5\cdot0.85^1+15\cdot0.85^2)\\\\\\P=0.00051(1+4.25+10.84)\\\\\\P=0.00051\cdot16.09\\\\\\P=0.008`