Answer:
a)
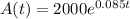
b)
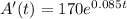
c)$3059.1808
d)t=4.77 years
e) The balance growing is $254.99/year
Explanation:
We are given that Two thousand dollars is deposited into a savings account at 8.5% interest compounded continuously.
Principal = $2000
Rate of interest = 8.5%
a) What is the formula for A(t), the balance after t years?
Formula
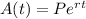
So,
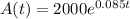
B)What differential equation is satisfied by A(t), the balance after t years?
So,
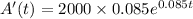
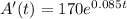
c)How much money will be in the account after 5 years?
Substitute t = 5 in the formula "

d)When will the balance reach $3000?
Substitute A(t)=3000
So,
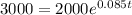
t=4.77
The balance reach $3000 in 4.77 years
e)How fast is the balance growing when it reaches $3000?
Substitute the value of t = 4.77 in derivative formula :
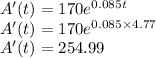
Hence the balance growing is $254.99/year