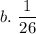Question

In a certain​ lottery, you must select 5 numbers​ (in any​ order) out of 26 correctly to win. a. How many ways can 5 numbers be chosen out of 26 ​numbers? b. You purchase one lottery ticket. What is the probability of​ winning? a. There are nothing different ways the numbers can be selected.

Answer 1

a. 7893600

`b.\ (1)/(26)`

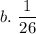
Explanation:

Given that there are 26 numbers out of which 5 numbers are to be chosen.

Here repetition is not allowed.

For each of the 5 cases, the total number of possibilities will keep on decreasing by 1.

1st case, number of possibilities = 26

2nd case, number of possibilities = 25

3rd case, number of possibilities = 24

4th case, number of possibilities = 23

5th case, number of possibilities = 22

a. Total number of possibilities = 26
`*`25
`*`24
`*`23
`*`22 = 7893600

b. Probability of winning by choosing one number:

Formula for probability of an event E can be observed as:
`P(E) = \frac{\text{Number of favorable cases}}{\text {Total number of cases}}`

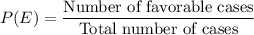
Number of favorable cases = 1

Total number of cases = 26

So, required probability:

`P(E) = (1)/(26)`

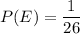
So, the answers are:

a. 7893600

`b.\ (1)/(26)`