Answer:
The cost difference would be of $22,067.5
Explanation:
In a sample with a number n of people surveyed with a probability of a success of
 , and a confidence level of
, and a confidence level of
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.

In which
z is the zscore that has a pvalue of
 .
.
The margin of error is:
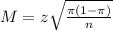
In this question, we have that:
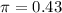
I think there was a small typing mistake, and the confidence level was omitted. I will use a 95% confidence level.
95% confidence level
So
 , z is the value of Z that has a pvalue of
, z is the value of Z that has a pvalue of
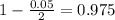 , so
, so
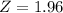 .
.
How many people are needed for a margin of error of 4 percentage points?
This is n when M = 0.04. So
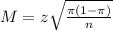
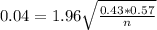
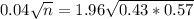

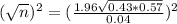

Rounding up
For a margin of error of 4 percentage points, 589 people will be sampled.
How many people are needed for a margin of error of 1 percentage point?
This is n when M = 0.01. So
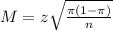
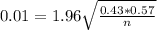
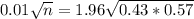

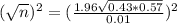

Rounding up
For a margin of error of 1 percentage point, 9416 people will be sampled.
What would be the cost difference for a poll designed to have a margin of error of 1 percentage point vs. that of a poll designed to have a margin of error of 4 percentage points?
Cost per person $2.50.
Margin of error of 0.01: Cost of 9416*2.50 = $23,540
Margin of error of 0.04: Cost of 589*2.50 = $1472.5
Difference:
23540 - 1472.5 = $22,067.5
The cost difference would be of $22,067.5