Question

A botanist wishes to estimate the typical number of seeds for a certain fruit. She samples 54 specimens and counts the number of seeds in each. Use her sample results (mean = 81.1, standard deviation = 8.4) to find the 90% confidence interval for the number of seeds for the species. Enter your answer as an open-interval (i.e., parentheses) accurate to 3 decimal places.

Answer 1

90% confidence interval for the number of seeds for the species

(78.8073 ,83.3927)

Explanation:

Step(i):-

Given sample size 'n' =54

Mean of the sample x⁻ = 81.1

standard deviation of the sample 'S' = 8.4

90% confidence interval for the number of seeds for the species

`(x^(-) -t_{(\alpha )/(2) } (S)/(√(n) ) , x^(-) -t_{(\alpha )/(2) } (S)/(√(n) ))`

Step(ii):-

Degrees of freedom

ν = n-1 = 54-1 =53

`t_{(0.10)/(2) } = t_(0.05) = 2.0057`

`(81.1 -2.0057(8.4)/(√(54) ) , 81.1 +2.0057(8.4)/(√(54) ))`

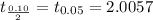
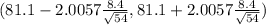
(81.1- 2.2927 ,81.1 + 2.2927 )

(78.8073 ,83.3927)

Final answer:-

90% confidence interval for the number of seeds for the species

(78.8073 ,83.3927)