Answer:
Option (2)
Explanation:
Given expression is, AX + B = C
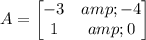
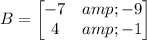
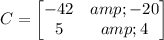
AX + B = C
AX = C - B
C - B =
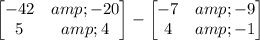 =
=
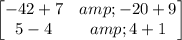
C - B =
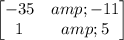
Let
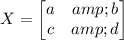
AX =
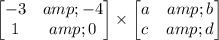
=
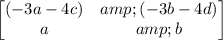
Since AX = C - B
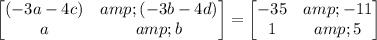
Therefore, a = 1, b = 5
(-3a - 4c) = -35
3(1) + 4c = 35
3 + 4c = 35
4c = 32
c = 8
And (-3b - 4d) = -11
3(5) + 4d = 11
4d = -4
d = -1
Therefore, Option (2). X =
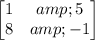 will be the answer.
will be the answer.