Question

A triangle has vertices A (-5, -4), B (2, 6), and C (4, -3). The center of dilation is the origin and (x, y) changes to (3x, 3y). What are the vertices of the dilated image?

Answer 1

(-15,12),(6,18)(12,-9)

Explanation:

Given

A (-5, -4), B (2, 6), and C (4, -3)

Dilated from (x,y) to (3x,3y)

Required

Vertices of the dilated image

First, the scale factor has to be calculated

This is calculated as thus;

Dilation = Original * Scale Factor;

In case of (x,y) to (3x,3y)

So, we have

`(3x,3y) = Scale\ Factor * (x,y)`

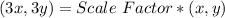
Simplify brackets

`3(x,y) = Scale\ Factor * (x,y)`

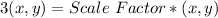
Divide both sides by (x,y)

`(3(x,y))/((x,y)) = (Scale\ Factor * (x,y))/((x,y))`

`(Scale\ Factor * (x,y))/((x,y))=(3(x,y))/((x,y))`

`Scale\ Factor =(3(x,y))/((x,y))`

`Scale\ Factor =3`

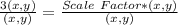
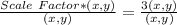
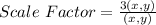
Now, the vertices of the new image can be calculated;

Using the formula: Dilation = Original * Scale Factor;

At vertex A(-5,4)

Dilation = (-5,4) * 3

Dilation = (-5*3 ,4*3)

Dilation = (-15,12)

At vertex B(2,6)

Dilation = (2,6) * 3

Dilation = (2*3 ,6*3)

Dilation = (6,18)

At vertex C(4,-3)

Dilation = (4,-3) * 3

Dilation = (4*3 ,-3*3)

Dilation = (12,-9)

Hence, the vertices of the dilated image are (-15,12),(6,18)(12,-9)