Question

Mark dropped an object from a bridge 400 feet above the ground level with an initial velocity of 0. He knows that the gravitational pull of the earth is about 16 feet per second squared. wants to find how many seconds,t, it will take the object to hit the ground. Match each expression with the correct equation that models this situation or solution.

Answer 1

correct equation: -16t^2 + 0t + 400 = 0

solution: 5 seconds

i just did the workbook and got it correct!

Answer 2

The first listed equation is the correct equation to solve

The correct answer is: t = 5 seconds

Explanation:

Let me mention first that there is an error in the statement that the gravitational pull of the Earth is 16 ft/s^2. It is in fact 32 ft/s^2, and the actual equation uses half of the acceleration multiplied by the square of the variable time, so it gives as final expression :

`y(t)=-16\,t^2+ 0 \,t +400`

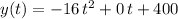
and we want to find the value/s for "t" that make this equation equal zero (when it reaches the ground and the object just touches the ground. This makes the equation we want to solve:

`0=-16\,t^2+ 0 \,t +400\\16\,t^2+0\,t -400=0`

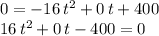
which solving for "t" becomes:

`16\,t^2-400 =0\\16\,t^2=400\\t^2=(400)/(16) \\t^2=25\\t= +/- 5\,\,sec`

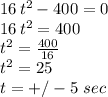
So we adopt the positive answer (positive time) since the negative value has no physical meaning for this problem.

That is: t = 5 seconds