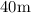Question

Ignoring air resistance and the little friction from the plastic tube, the magnet was a freely-falling object in each trial. If a freely-falling object is travelling twice as fast after it has fallen 40 m than after falling 10 m, what do you predict the maximum emf would be if you drop the magnet through the same coil from a height of 40 cm? Explain your answer.

Answer 1

emf will also be 10 times less as compared to when it has fallen
`40 \mathrm{m}`

Step-by-step explanation:

We know, from faraday's law-

`e m f=-N (\Delta \Phi)/(\Delta T)`

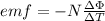
and
`\Phi=B . A`

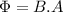
So, as the height increases the velocity with which it will cross the ring will also increase.
`(v=√(2 g h))`

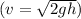
Given

`\mathrm{V} 1(\text { Speed at } 40 \mathrm{m})=2 \mathrm{x} \mathrm{V} 2(\text { speed at } 10 \mathrm{m})`

`\sqrt{2 g h_(2)}=2 * \sqrt{2 g h_(1)}=28.28 \mathrm{m} / \mathrm{s}`

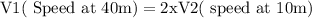
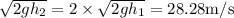
Now, from
`40 \mathrm{cm}`

`V_(3)=\sqrt{2 g h_(3)}=√(2 * 10 * 0.4)=2.82 \mathrm{m} / \mathrm{s}`

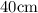
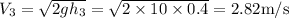
From equation a and b we see that velocity when dropped from
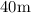`40 \mathrm{m}` is 10 times greater when height is 40
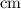`\mathrm{cm}` so, emf will also be 10 times less as compared to when it has fallen
`40 \mathrm{m}`