Question

The dilation of ΔABC by a scale factor of 2 with a center of dilation at (-4,-9). A (-4,-6), B (3,-6), and C (-2,-1). What is the coordinate of C'?

Answer 1

The coordinate of C' is (0,7).

Explanation:

Relative coordinates of each point of the ABC-Triangle are obtained first:

`A_(rel) = A - O_(dil)`

`B_(rel) = B - O_(dil)`

`C_(rel) = C - O_(dil)`

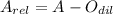
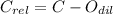
Where:

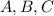`A, B, C` - Absolute coordinates of the vertices of the ABC-Triangle.

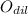`O_(dil)` - Coordinates of the center of dilation.

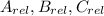`A_(rel), B_(rel), C_(rel)` - Relative coordinates of the vertices of the ABC-Triangle.

If
`O_(dil) = (-4, -9)`,
`A = (-4, -6)`,
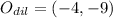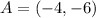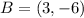`B = (3, -6)` and
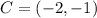`C = (-2, -1)`, the relative coordinates are now computed:

`A_(rel) = (-4,-6) - (-4,-9)`

`A_(rel) = (-4 + 4, -6 + 9)`

`A_(rel) = (0, 3)`

`B_(rel) = (3, -6) - (-4,-9)`

`B_(rel) = (3+4, -6 +9)`

`B_(rel) = (7,3)`

`C_(rel) = (-2, -1) - (-4,-9)`

`C_(rel) = (-2+4, -1 +9)`

`C_(rel) = (2, 8)`

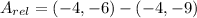
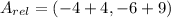
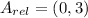
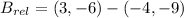
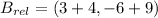
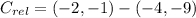
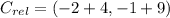
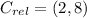
Each outcome is consequently dilated:

`A'_(rel) = 2\cdot (0,3)`

`A'_(rel) = (0,6)`

`B'_(rel) = 2 \cdot (7,3)`

`B'_(rel) = (14, 6)`

`C'_(rel) = 2 \cdot (2,8)`

`C'_(rel) = (4,16)`

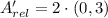
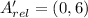
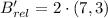
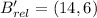
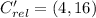
The absolute coordinates of A', B' and C' are, respectively:

`A' = O_(dil) + A'_(rel)`

`A' = (-4,-9) + (0,6)`

`A' = (-4+0, -9 + 6)`

`A' = (-4, 3)`

`B' = O_(dil) + B'_(rel)`

`B' = (-4,-9) + (14,6)`

`B' = (-4+14, -9+6)`

`B' = (10, -3)`

`C' = O_(dil) + C'_(rel)`

`C' = (-4,-9) + (4,16)`

`C' = (-4 + 4, -9 + 16)`

`C' = (0, 7)`

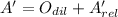
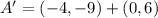
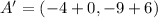
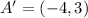
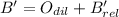
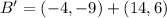
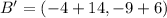
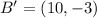
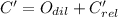
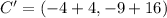
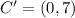
The coordinate of C' is (0,7).