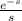Question

Let f be a function defined for t ≥ 0. Then the integral ℒ{f(t)} = [infinity] e−stf(t) dt 0 is said to be the Laplace transform of f, provided that the integral converges. to find ℒ{f(t)}. (Write your answer as a function of s.) f(t) = cos(t), 0 ≤ t < π 0, t ≥ π

Answer 1

L(f(t)) =
`2 (e^(-s) )/(s) - (1)/(s)`

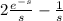
Explanation:

let f be a function defined for t ≥ 0

we can write the function f(t) in terms of unit function as follows

f(t) = 2 u,(t) - 1 where

0≤ t < 1

f(t) = (2 * 0) -1 = -1

when t ≥ 1

f(t) = (2*1 )- 1 = 1

Now the Laplace transform L(F(T)) = 2L( u, (t) ) - L(1) --------equation 1

this is because L(u,(t)) =
`(e^(-cs) )/(s)`

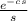
c = 1 hence L(1) = 1/s

back to equation 1

L(f(t)) = 2
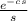`(e^(-cs) )/(s)` - 1/s laplace transform

also L(u(t) ) =
`(e^(-s) )/(s)`