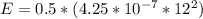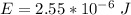Answer:
The charge stored is
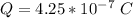
The energy stored is
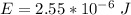
Step-by-step explanation:
From the question we are told that
The area of the plates is
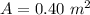
The separation between the plate is

The potential difference is
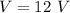
The permitivity of free space is
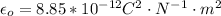
The dielectric constant of glass is K = 5.0
Generally the capacitance of this capacitor is
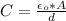
substituting values
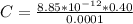
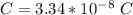
The charge stored is mathematically evaluated as

substituting values

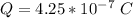
The energy stored is
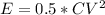
substituting values