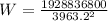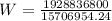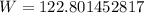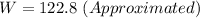Answer:
Her weight is approximately 122.8lb
Explanation:
Given
Inverse proportion;
Weight = 123lb when distance = 3960 miles from center of earth
Required
Calculate the weight when distance is 3.2 miles above sea level
Let weight be represented by W and distance by D
From the question, we understand that;
Weight is inversely proportional to square of distance;
Mathematically; this is
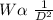
Convert proportion to equation
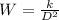
Where k is the constant of proportionality
When W = 123; D = 3960.
This implies that

Make k the subject of formula


Calculating her weight when she's at the top of mountain, 3.2 miles above sea level
First, her distance from center of earth has to be calculated
Distance = Previous distance + 3.2
Distance = 3960 + 3.2
Distance = 3963.2
Now, her weight can be calculated using
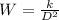
Substitute for k and D